Stochastic Modeling

Broadly stated, Stochastic Modeling involves applying a wide range of probabilistic techniques to try to determine an optimal solution to a problem that involves a great deal of uncertainty and is too complex, too time consuming, and, perhaps most importantly, too expensive to realistically find an exact solution to.

Applied in a business setting, Stochastic Modeling takes into account the risk caused by real-world randomness inherent in making tough business decisions. For example, no prudent business owner would order next year's inventory based solely upon what happened this year. The coming year is full of uncertainties, e.g., an unforeseen change in demand, sudden hike in interest rates, tariffs, unexpected materials shortage, et cetera. And he certainly wouldn't buy inventory to meet each possible situation. The goal of applying Stochastic Modeling to business is to determine that course of action to take that, taking real-world uncertainties in account, will reap the greatest profit with the least amount of risk.

Stochastic Modeling can also be applied to situations where a business owner could find the "exact", most cost effective course of action to take but determining that course of action would be untenable due to complexity, cost, and time. A classic example of this is Route Cost Minimization, commonly referred to as " The Traveling Salesman Problem" ( for the curious click Traveling). In this situation Stochastic Modeling has the ability to determine a nearly exact solution to the problem.

One of the basic "foundations" of Stochastic Modeling is Monte Carlo Simulation. This analytic technique was invented during the Manhattan Project to determine the outcome of various proposed theories without incurring the cost, time, and complexity of building a new atom bomb to test each new theory. At the heart of Monte Carlo Simulation is the use of a real-world random process - such as flipping a coin - to achieve a non-random, deterministic result. The following imaginary problem captures the essence of Monte Carlo Simulation.

A Fishy Problem

Consider the following: Suppose you own a sport trout fishing business consisting of a large parcel of rectangular land enclosing a very irregularly shaped lake - Figure 1. below:

To prepare for the coming season you must determine how many trout to stock the lake with. Too few and you lose money, too many and they die off from overcrowding. Now suppose a proven formula exists that tells you the optimal (i.e., most profitable) number of trout to stock the lake with based on the surface area of the lake. Obviously your goal is to determine the surface area of your lake.

The conventional approach would be to hire a surveyor to employ highly sophisticated and complex laser measuring techniques. Unfortunately time is of the essence and the surveyor is booked solid for the next month and even if he weren't, his fees are beyond your means. Here you have the classic elements of a problem tailor made for the application of Monte Carlo Simulation - great complexity, time is of the essence, and high cost.

The Stochastic Solution

The key to solving our trout stocking problem is to view it in a Stochastic (i.e., probabilistic) framework using Monte Carlo Simulation. Suppose you stand outside the rectangular border with a pneumatic tennis ball serving machine and a supply of 1000 tennis balls. The machine is special in that the velocity and direction of each ball fired into the rectangle are wholly random and therefore each ball has an equal chance of landing anywhere inside the rectangle - on the land or in the lake.

After 10 shots, the result could look like Figure 2. below:

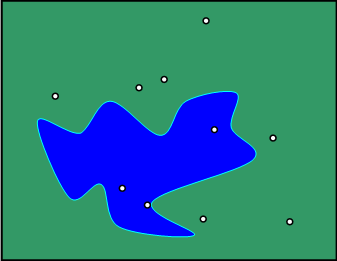After 100 shots, like Figure 3. below:

At this point 23 balls have landed in the lake. The resulting ratio of balls that have landed in the lake versus total balls shot into the rectangle is 23/100=23%. If the rectangle covers 6 acres in total then the lake, at this point in the simulation, covers about 23% of the total area or about 1.4 acres (.23 x 6 acres = 1.4 acres).

You launch the remaining 900 tennis balls. For argument's sake let's say that the final count of balls landing in the water is 256 resulting in a ratio of 256/1000 = 25.6% and a more precise estimate of the lake surface at 1.54 acres (.256 x 6 acres = 1.54 acres). Want an even better approximation? - then launch another 1000 tennis balls. You get the idea - the more you launch the more precise the area of the lake will be. When should you stop? When the cost of launching and counting become prohibitive.

The results obtained above may seem counterintuitive: we used a random event, shooting tennis balls into the rectangle, to obtain a deterministic result, the lake's acreage. Yet this logic is no different than that used to determine if a pair of dice are loaded. Let's suppose you feel that the dice being used in a game come up with a face value of 11 more often then they should. You could cut the dice in half to discover if they have been modified. Or, on a less destructive note, you could roll the dice 1000 times and note how often 11 comes up. The odds of throwing an 11 is 2 out of 36 or about 5.6%. So, if after 1000 rolls the number of times 11 comes up is substantially greater than 56 times (2/36 x 1000 = 55.555...), you can be rather confident that the dice are loaded. Random event, rolling dice, deterministic result, dice are loaded.

Stochastics And The Real Business World

The important point here is that Stochastic Modeling techniques can be applied to those business situations where precise (i.e., deterministic) results are very difficult to obtain due to cost, time, complexity, and, most dangerous of all, the uncertainty inherent in the business world. Consider the real-world business situation described below where making the most cost effective decision is a challenge due to uncertainty:

A large precision parts manufacturing company runs 10 high-end drill presses on a continuous basis. Every hour a drill press is down costs the plant $200. A new press costs $5000. A planned replacement will take the press out of operation for 2 hours. When a drill press fails unexpectedly and needs to be replaced the downtime is 20 hours. A used press has a salvage value based on its condition. The two possible courses of action are:

1) replace all drill presses on a regular basis or

2) wait for the inevitable failure of each press and replace them then.

The solution to the problem is too complex to go into here due to the implementation of various probability functions such as Weibull, Poisson, etc. The point here is that this is precisely the kind of real world business situation where the decision to go ahead is fraught with uncertainty - a perfect situation for implementing Stochastic Modeling. For the curious reader: replacing drill presses after 80hrs. of operation minimizes expected cost.

Since 2001 we have proven that applying Stochastic Modeling techniques assures the small business owner that he is taking the most profitable course of action possible when confronted with the randomness inherent in making a critical business decision.

back